「暦」の工夫

勉強部屋・特別編。「暦を知ろう」シリーズです。
♪ 夏も近づく八十八夜
野にも山にも若葉が茂る
あれに見えるは茶摘みぢやないか
あかねだすきに菅(すげ)の笠
5月2日は「八十八夜」です。これも実は季節を表すコトバ。
というわけで、不定期で「季節の節目」にやってる勉強部屋・特別編「暦を知ろう」シリーズです。
間が空いてるので、少しおさらいしながら行きましょう。
前回、「季節の一巡り」が「太陽の動きの周期」と関係していることを紹介しました。
今回はこれを「暦」に反映し、補正を利かせた「太陰太陽暦」が出来上がるまでをご紹介。
前回までのおさらい
「太陽太陰暦」とは何か。
月の満ち欠けによって、時間の経過を計る方法として「太陰暦」が考え出されましたが、これでは「1年の長さ」を正確に測ることが困難である、徐々に季節がズレていく、ということを最初にお話ししましたね。
そこで、太陽の動きを観測し、それをもとに1年の長さを決めることで、季節のめぐりが分かる、というところまでが前回のお話。
もう一度、整理しましょう。
ひと月の長さは「月が満ち、かけてゆく」というサイクル。月の始まりは「新月(朔)」から始まり、このサイクルは大体29.5日でまた「新月(朔)」が巡ってきます。
キレイに割り切れないのですが、大の月(ひと月が30日間)と、小の月(ひと月が29日間)を交互に繰り返していけば、おおよそ月の運行と「ひと月の長さ」の補正が取れます。
一方、1年の長さ(季節の一巡り)は、太陽の高さ(太陽黄道の角度)の変化のサイクルです。このサイクルは大体356.25日。
この周期は「太陰暦による12か月(354日)」と近しい数字なのですが、厳密には11日程度ズレています。
さて、このズレをいかにして補正を掛けていくか。これが太陽太陰暦のポイントであり、季節というものを深く知るための鍵でもあるのです。
まずは季節のめぐりを正確に測ろう
太陽太陰暦ができる前段階として、まず太陽の運行、季節のめぐりを正確に測る必要があります。
「月が満ちて欠ける」1サイクルは、「新月(朔)」が基準点となったように、太陽もどこか基準となるポイントが無いか。
そこでまず「夏至」と「冬至」が生まれるのです。1年の中で、「最も日が高く昇る時」と「最も日が低く昇る時」は、影の長さが最も短くなる日と、最も長くなる日ですので、観測が比較的容易です。
観測のしやすさでいえば、「春分」と「秋分」も観測がしやすい日でしょう。太陽が「真東から昇り、真西に沈んでいく日」は、1年の中でこの春分と秋分の2回、起こるのです。
「夏至と冬至」を二至、「春分と秋分」を二分、と呼び、これら4つの太陽の位置を合わせて二至二分(にしにぶん)と言います。
実は1年の長さをだいたい4等分したものが、この二至二分に相当します。
ただ、春夏秋冬という四季は、「いまから夏です!」「後何日で冬が終わります!」といったように、キッチリと分かれているわけではありませんよね。
季節は徐々に変化していくものであり、暑かったり寒かったりを繰り返しながら、緩やかに移ろい行くものです。
二至二分だけでは、まだ「今の季節」がわかりづらい。そこで二至二分のそれぞれの中間地点、つまり1年の長さをさらに細かく分割してみましょう。
「春分と夏至の中間地点」は立夏。
「夏至と秋分の中間地点」は立秋。
「秋分と冬至の中間地点」は立冬。
「冬至と春分の中間地点」は立春。
これらを「四立(しりゅう)」と呼び、先ほどの二至二分と四立をあわせて、8つの節目、ということで「八節(はっせつ)」という考え方が生まれました。
太陽太陰暦ができる前までは、これらの季節の基準点を独自に観測し、太陰暦とは別のモノサシとして計っていた時期があったようです。
算数のお時間です
季節を知るための目安として、「八節」という考えが生み出されました。ここで整理してみましょう。
1年の長さは大体365.25日、まあ分かりやすく整数に直して「365日」ということがわかりました。
その1年の長さを分かつポイントとして、太陽の高さを基準にした「八節」という考えを元に、「この間隔が何日間隔なのか」というところにスポットを当ててみましょう。
「冬至と夏至」が1年の長さの大体半分。つまり「冬至→夏至」の間隔は、約182日で巡ってきます。
二至二分は1年の長さの大体四分割。ということは、「夏至→秋分」の間隔は、約91日で巡ってきます。
八節は1年の長さの大体八等分。ということは、「秋分→立冬」の間隔は何日でしょうか・・・答えは約45日。
何とか、この大要を基準にした「八節」と、月の運行を基にした太陰暦を組み合わせて、便利に季節を知りたい!
とうとう来ちゃった、数学のお時間です。

みなさん、数学は好きですか?アレルギー反応を起こした方は、深呼吸して落ち着いてください(笑)
365日の1年を、「なんとかして12ヶ月に対応させよう」とすると、1月の長さは約30日。でも、月の運行では小の月(ひと月が29日間)の月があるため、微妙に違います。
あくまでも「月の満ち欠けが絶対」という条件なので、月の長さは変えられない。ではどうするか。
「もっとも季節(太陽の運行)とのズレが大きくなったところで、閏月(補正する月)を挿入する」という、飛び道具を使うのです。
要(かなめ)となるは、この「閏月を挿入するタイミング」をどうやってきめるか、です。
具体的な数字と例を出しながら、考えてみましょう。
仮に「太陽が真東から昇って、真西に沈む春分」を基準として、1年のちょうど半分が経ったとします。
太陰暦では、大の月(30日間)→小の月(29日間)の繰り返しで月を重ねていくので、1年の半分、つまり6ヶ月だと177日が経過しています。
しかし季節のめぐりは「まだ1年の半分ではない」のです。
1年の半分であれば、また太陽は真東から昇るはず(秋分)なのに、177日目の太陽はちょっと位置がずれてる。上で紹介したように、春分→秋分の間隔は182日であり、実際の季節のめぐりよりも5日早く、太陰暦では「半年」を数えているのです。
「よーし、実際の季節よりも5日早まってるから、ここで閏月(30日の1か月)を挿入しよう」
すると、どういうことが起こるか?
今度は「閏月が終わった時点で、実際の季節が遅れる(実際の季節よりも暦が進みすぎる)」という事態が起こるのは、簡単に想像つきますよね?
もっともベストなタイミング、つまり暦と実際の季節のズレが「30日程度」に広がった段階で、閏月を挿入したい…。
んー、太陰暦(12か月)と八節(8つのチェックポイント)だけでは、まだまだズレの補正が効かせにくい。どうするか?
天才的発想(チョコレートケーキの話)
12と8の最小公倍数……「24」。(24…どこかで聞いたような、どこかで見たような?)
これを考えるに至った原初の人類の発想力に敬服いたします。
何が言いたいかというと、この「12か月」と「八節」を対応させるための力業ともいえるのがこの最小公倍数なのです。
なんだが仰々しいので、話を小学校の算数っぽく例えましょうか。
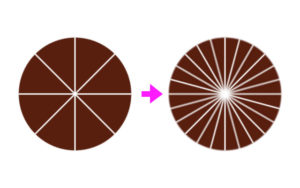
すでに8等分されたチョコレートケーキがあったとします。
12人のお友達でケンカにならないよう、これをきれいに分けたい。どこで切れ目を入れればいいかな?
こたえはココ!
8等分された一切れを、ちょうど3等分すると…1切れがケーキ全体を24等分した大きさになる。
これを「1人2切れ」で分ければ、みんなそれぞれ同じ分量になり、ケンカも起こりませんね~。
話を暦の話に戻すと…まずは八節の間隔を思い出してください。
八節は1年の長さの大体八等分。ということは、「秋分→立冬」の間隔は何日でしょうか・・・答えは約45日。
45日。なんとこれがぴったり3等分できる数字なんです。季節と季節の「中間地点」をずっと半分にしてきましたが、ここだけ三分割します。
そうすると、1年の長さを24分割できます。どこかで聞きましたよねー。ここでようやく二十四節季が完成します。
二十四節季は「12か月の月ごとに、節季が2つずつ含むようにする」という工夫のために考え出されたモノサシなのです。
このモノサシ、どうやって使う?

人類の英知が生み出した「二十四節季」という魔法のモノサシ。これを使えばたちどころに季節のズレが分かっちゃう。
まずは今まで通り、太陰暦にのっとって、「朔日(新月の日)」を月の始まりとして、日数をカウントします。
月の満ち欠けとは関係なく、太陽の運行(太陽黄道の角度)は変化するので、一ヶ月の間に「ある節季」を迎えます。
二十四節季の「ある節季から次の節季まで」の間隔は15日間なので、一ヶ月の間に2つの節季(せっき)が来るはずです。
しかし月の運行(月の満ち欠け)の周期は「約29.5日」なので、大の月(30日間の一ヶ月)と小の月(29日間の一ヶ月)を繰り返しているうちに「節季が1つしかない月」もしくは「節季が3つも来ちゃう月」が発生します。
ここが「閏月の挿入ポイント」なのです。この「節季が2つじゃない月」の出現は、暦の運行と実際の季節のズレが30日分たまった事で発生するので、「節季が2つじゃない月」の次の月を「閏月」とします。
閏月にももちろん節季は出現しますが、イレギュラーな節季の月になるはずです。(閏月の前の月が「節季が2つじゃない」ので、その帳尻合わせがこの閏月で行われる)
そして、閏月が終わった次の月からは、また通常通りの「節季が2つある月」が続いていきます。
これでも随分と端折りながら、駆け足なんですよ?ここまで来るのが長かった…。
次回はこの二十四節季を細かく見ていきましょう。